Fibering of the trefoil knot complement

I’ve found myself re-calculating the fibration of the trefoil knot complement again, so I thought I’d write a short note this time to record it. The main technique is the elastic cord criterion from

Sebastian Baader and Christian Graf, Fibred links in $S^3$, Expo. Math. 34 (2016), no. 4, 423–435. doi:10.1016/j.exmath.2016.06.006 MR 3578006

What is a fibered knot?

An oriented knot (or link) $K\subset S^3$ is called a fibered knot if the knot complement $S^3-K$ can be given the structure of a fibration over $S^1$ such that the closure of each leaf is a compact oriented surface whose boundary is $K$ with the correct induced orientation. In other words, there is a smooth map $f:S^3-K\to S^1$ with no critical points such that the closure of $f^{-1}(\theta)$ is a Seifert surface for $K$ for each $\theta\in S^1$. Letting $\Sigma=f^{-1}(0)$ be one of the fibers, circle-valued functions like this generate a smooth map $\mu:\Sigma\to\Sigma$ called the monodromy, which is obtained through gradient flow: we can use $df$ to pull $d\theta$ back to $S^3-K$ then use the metric to form a non-vanishing vector field, and then $\mu(x)$ is given by an integral curve starting at $x$ then seeing where it ends up at time $t=2\pi$. The monodromy lets us regard $S^3-K$ as a mapping cylinder of $\Sigma$:

$$\begin{align*} S^3-K \approx (\Sigma\times [0,1])/({(\mu(x),0)\sim (x,1)}) \end{align*}$$ As a smooth oriented manifold, this only depends on the isotopy class of $\mu$.

The knot exterior (the complement of a tubular neighborhood of $K$) is given by the same mapping cylinder construction but with a compact oriented surface. In the above construction, one can arrange for the monodromy to be the identity in a neighborhood of $K$ since, near $K$, the flow of a point in $\Sigma$ gives a meridian loop:

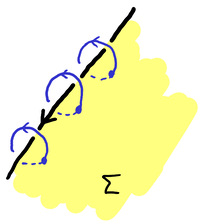
The main takeaway of all this is that “calculating the fibering” amounts to giving the following data: (1) a compact oriented surface $\Sigma$ and (2) a smooth map $\mu:\Sigma\to\Sigma$ that is the identity when restricted to the boundary.

Since it’s the identity on the boundary, the map extends to a smooth map of a closed oriented surface obtained by collapsing each boundary curve to a point. From this point of view, the data is (1) a closed oriented surface $\Sigma$ with a finite collection of points and (2) a smooth map $\mu:\Sigma\to\Sigma$ that fixes each point in the collection. Incidentally, this gives a fibering of the $0$-surgery of the knot or link.

What is the elastic cord criterion?

Let’s consider the case of a knot exterior, so $\Sigma$ is compact. An observation for a fibration is that if you find a cut set of arcs for $\Sigma$, you can flow the arcs themselves from $\Sigma$ to $\Sigma$, giving properly embedded squares $[0,1]\times[0,1]$ in $\Sigma\times[0,1]$ such that ${0,1}\times[0,1]$ is embedded “vertically”, and the complement of the squares in $\Sigma\times[0,1]$ is a disjoint union of open balls.

Conversely, given a (connected^[1]) Seifert surface $\Sigma$ for an oriented knot (or link) $K$, if one can find a cut set of arcs for $\Sigma$ along with disjoint properly embedded squares in $S^3-\nu(K)$ whose “vertical” boundaries are meridians for $K$, then because knot complements are irreducible the complement of the union of $\Sigma$ and the squares is a disjoint union of open balls, and hence $K$ is fibered.

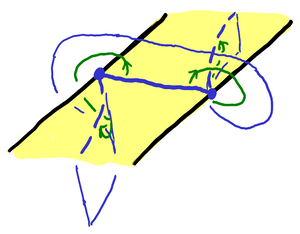
It turns out that you don’t need to actually worry about the disks themselves. The elastic cord criterion is that a knot (or link) $K$ is fibered if and only if there is a Seifert surface with a cut set such that, with the arcs being thought of as “elastic cords” attached to the boundary on one side of the surface, they can be dragged to the other side. The monodromy is determined by where the cords end up. (Also, if there is any arc that, as an elastic cord, cannot be dragged to the other side, the knot is not fibered.)

Here’s an attempt at illustrating an elastic cord (blue thick line) being dragged in the direction of the green arrows to the other side of the surface (dashed blue thick line), with a portion of the square it is dragged through:

The trefoil knot

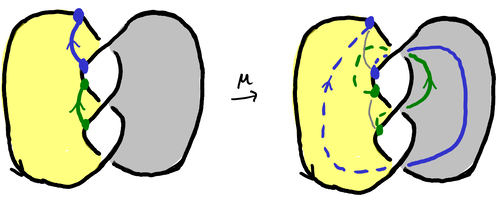
The (right-handed) trefoil knot has a genus-$1$ Seifert surface from taking one of the two checkerboard surfaces from a standard diagram. Here’s an illustration of the Seifert surface (yellow is the front side, gray is the back), a cut set of arcs given by the blue and green curves, and the the result of taking the arcs as elastic cords and dragging them to the other side of the surface:

Since this could be done, we see the trefoil knot is be a fibered knot by the elastic cord criterion. I want to get this into a good position to understand the monodromy, so as a first step we’ll cut along the cut set and twist the surface to lay it out flat: Then I’ll un-distort the second diagram: This gives a monodromy, but I want to get to a really nice description of it. One thing we can do is turn this into an ideal triangulation, essentially by gluing a disk into the boundary. When it’s an ideal triangulation, it’s more obvious that the image of the green arc is isotopic to the blue arc with reversed orientation: Now, we’ll draw this on the universal cover of the torus: The doubled arrows represent what the monodromy does to the blue and green arcs, and the dotted blue arc is sent to the green arc by the monodromy. As we can see, on this universal cover, the monodromy is a rotation by $60$ degrees clockwise about any of the lifts of the ideal point!

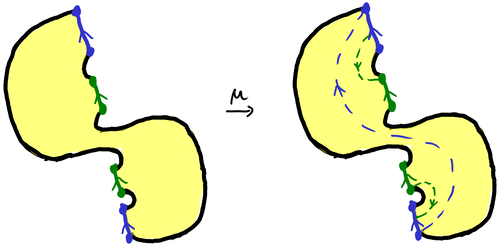
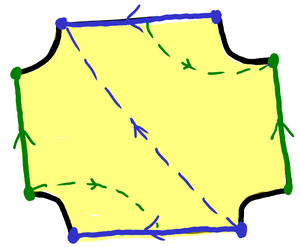
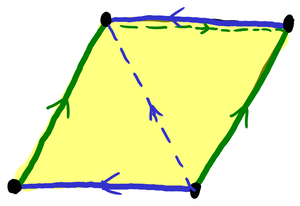
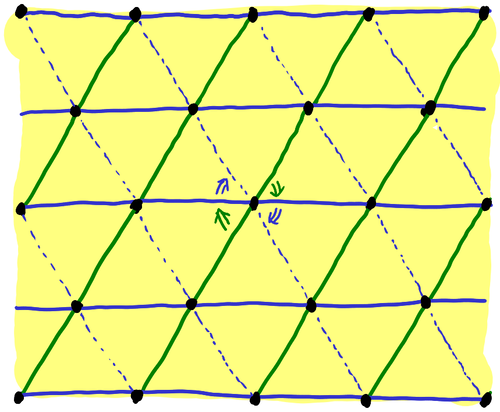
The lattice of lifts of the ideal point can be described as $\Z[\omega]\subset\C$ with $\omega=e^{\pi i/3}$, and then the covering map is given by $\C$ modulo $\Z[\omega]$ as abelian groups. The action of $\omega^{-1}$ on $\C$ by multiplication descends to the quotient, which is a torus. The image of $0$ is fixed by the action and corresponds to the ideal point.

Using the $\{1,\omega\}$ coordinate system, the matrix of the $\omega^{-1}$ action is

$$\begin{align*} \begin{bmatrix} 1 & 1 \\ -1 & 0 \\ \end{bmatrix} \end{align*}$$ This can be used as the matrix for the induced action of the monodromy on $H_1(\Sigma)$ for $\Sigma$ the fiber surface (this is by the duality between $H_1(\Sigma,\partial\Sigma)$ for arcs in the cut set and $H_1(\Sigma)$ via the intersection form). The Alexander polynomial of a fibered knot can be calculated from the characteristic polynomial of the induced action on $H_1(\Sigma)$, which in this case is the expected $1-t+t^2$.

The left-handed trefoil knot is similar, but instead the monodromy corresponds to a $60$ degrees counterclockwise rotation.