Four-coloring infinite graphs

The four-color theorem states that every planar loopless graph can be four colored. That is, there is an assignment to each vertex of one of four distinct “colors” such that adjacent vertices are assigned distinct colors. The case of finite graphs was proved by Appel and Haken in 1976 with computer assistance (with some errors corrected in 1989), and in 2005 Werner and Gonthier formalized a proof of the theorem inside the Coq proof assistant.

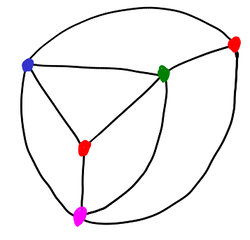
A remarkable fact is that the case of infinite graphs follows from the finite case as a matter of pure logic. All you need to extend to infinite graphs is the fact that subgraphs of planar graphs are planar! This was originally proved by De Bruijn and Erdős in 1951.

In this post, we’ll go through a few ways of organizing the ideas for four coloring infinite graphs. It should be said that they are all highly non-constructive. While there might be some comparison to a limiting process, it would be at the level of colorings themselves — the limit does not descend to the level of the individual edges being colored, since the color assignments to an edge do not necessarily eventually stabilize in any way.

1. With model theory

There is a straightforward way to encode the four coloring problem using first-order logic, and then the infinite case follows immediately from the Compactness theorem. But first, we need a few definitions.

A signature consists of a collection of abstract sets called domains and a collection of abstract relations on these domains of any arity. By convention, unary relations are known as predicates. A theory for a signature is a collection of first-order sentences, where the quantifiers range over domains.^[1] The theory might include sentences that imply certain relations are functions, in such a case we will write $y=f(x)$ rather than, say, assert that $f(x,y)$ is true. A model for a theory is an assignment of concrete sets and relations for the signature that satisfy the theory.

The Compactness Theorem states that if every finite subset of a theory has a model, then the whole theory has a model. The argument here is surprisingly straightforward, which we will sketch because it’s kind of cool. Let $T$ be the theory, and let $\mathcal{F}T$ denote the set of all finite subsets of $T$. By assumption, each $I\in\mathcal{F}T$ has a model $M_I$. We construct a filter on $\mathcal{F}T$ (that is, on the poset $\mathscr{P}(\mathcal{F}T)$ of all subsets of $\mathcal{F}T$) generated by elements of the form

$$\begin{equation*} A_I := \{J\in\mathcal{F}T : I\subseteq J\} \in \mathscr{P}(\mathcal{F}T) \end{equation*}$$ for all $I\in\mathcal{F}T$. These elements satisfy the finite intersection property since $A_{I}\cap A_{J} = A_{I\cup J}$ for all $I,J\in\mathcal{F}T$, so the resulting filter is proper. By Zorn’s lemma, the filter extends to an ultrafilter $U$ on $\mathcal{F}T$ (ultrafilters are defined in the next section). For $\phi\in T$, we have $$\begin{equation*} B_\phi := \{I\in\mathcal{F}T : \phi\text{ is true in }M_I\} \supseteq \{I\in\mathcal{F}T : \phi\in I\} \supseteq A_{\{\phi\}}. \end{equation*}$$ Since $A_{\{\phi\}}\in U$, then $B_\phi\in U$ as well. Thus, by Łoś’s theorem^[2] the ultraproduct $M=\left(\prod_{I\in \mathcal{F}T} M_I\right)/U$ is a model for $T$. (By definition, $\phi\in T$ is true in $M$ iff $B_\phi\in U$.)

Ok, so how do we apply the compactness theorem? Let $G$ be a loopless planar graph with vertex set $V(G)$. Define a signature with domains $V$ and $C$ and a function $f:V\to C$. For each $v\in V(G)$, throw in constants $n_v\in V$ (i.e., nullary functions $n_v:()\to V$). Define a theory $T$ by having, for each edge $(v,w)\in E(G)$, the axiom $f(n_v)\neq f(n_w)$, and add in the additional axiom that $C$ has at most four elements.^[3]

Each finite subset of $T$ corresponds to some finite subgraph of $G$. Since finite subgraphs are, by assumption, four-colorable, the finite subset has a corresponding model. Hence, the compactness theorem says there is a model for $T$ itself. The domain $V$ in this model might have no relation to $V(G)$ (and in fact the ultraproduct construction will have constructed an absurdly large four-colored graph), but we may use the nullary functions to get a handle on things, since we may color $v\in V(G)$ by the color $f(n_v)$. Since we had the axiom that $C$ have at most four colors, we are done!

Remark. Except for the assertion that $C$ have at most four elements, none of the axioms really involve quantifiers (there are some hidden in the function applications, but by using four mutually exclusive proposition variables per vertex these could be eliminated). It would suffice to use the compactness theorem for propositional logic rather than the full compactness theorem for first-order logic.

2. With ultrafilters

The compactness theorem is worthwhile to know, but it can be illuminating to expand things out to see how the pieces fit together. Luxemburg^[4] essentially gave this argument in 1962.

Recall that an ultrafilter $U$ on the poset $\mathscr{P}X$ of subsets of a set $X$ is a subset of $\mathscr{P}X$ satisfying the following axioms:

1. If $A,B\in U$, then $A\cap B\in U$.
2. If $A\subseteq B\subseteq X$ and $A\in U$, then $B\in U$.
3. $\emptyset\not\in U$.
4. If $A\subseteq X$, then either $A\in U$ or $X-A\in U$.

An ultrafilter is a consistent choice of what are the “big” subsets of $X$. The intersection of big subsets is big, the superset of a big subset is big, the empty set is not big, and every set or its complement is big. One can check the intersection of a big set and a small set is small. In other words, there is a homomorphism from $(\mathscr{P}X,\cup,\cap)$ to the boolean lattice $(\{0,1\},\vee,\wedge)$.

A use of (ultra)filters in topology is generalized limits. An (ultra)filter $U$ on a topological space $X$ is said to converge to a point $x\in X$ if for all open sets $V\subseteq X$ containing $x$ then $V\in U$. The ultrafilter convergence theorem states that (1) $X$ is compact iff every ultrafilter converges to at least one point and (2) $X$ is Hausdorff iff every ultrafilter converges to at most one point.

Example. Given an index set $J$, consider the space $X=\{0,1\}^J$ with the product topology, which is compact by Tychonoff’s compactness theorem. For every finite subset $I\subseteq J$, the set

$$\begin{equation*} V_I = \{ x\in X : x_i=1 \text{ for all } i\in I\} \end{equation*}$$ is an open. Furthermore, for every pair of finite subsets $I_1,I_2\subseteq J$, we have $V_{I_1}\cap V_{I_2}=V_{I_1\cup I_2}$, so the collection $\{V_I:I\subseteq J\text{ is a finite subset}\}$ satisfies the finite intersection property. Collections that do not contain the empty set and that satisfy the finite intersection property extend to an ultrafilter; let $U$ be such an ultrafilter on $\mathscr{P}X$ extending this collection. Hence, by the ultrafilter convergence theorem, there is unique point $x\in X$ that $U$ converges to since the product of Hausdorff spaces is Hausdorff. This point is just the all-ones point $(1)_{i\in J}$.

Example. Let $M$ be a manifold and $C(M)$ the $\mathbb{R}$-algebra of continuous functions $M\to\mathbb{R}$. If $\mathfrak{m}\subset C(M)$ is a maximal ideal, then consider the collection of sets $f^{-1}(0)$ for $f\in\mathfrak{m}$. Since $\mathfrak{m}\neq C(M)$, we know none of these is the empty set. And, for $f,g\in\mathfrak{m}$, one can construction a function $h\in\mathfrak{m}$ with $f^{-1}(0)\cap g^{-1}(0)=h^{-1}(0)$ since manifolds have bump functions. Hence, the collection extends to an ultrafilter. If $M$ is compact, then the ultrafilter has a limit point $a\in M$ and thus $\mathfrak{m}$ is principal and generated by the function $x\mapsto x-a$, and hence the quotient map $C(M)\to C(M)/\mathfrak{m}$ is equivalent to the evaluation map $f\mapsto f(a)$.

Gottschalk’s argument^[5] for colorings of infinite graphs uses compactness. It is somewhat overkill to use ultrafilters here, but it doesn’t hurt to use the language. Given a loopless graph $G$ and a finite set $C$ of colors such that every finite subgraph of $G$ is $C$-colorable, let $X=C^{V(G)}$ be the set of all assignments of colors to vertices of $G$, endowed with the product topology. For each finite subset $I\subseteq E(G)$, define $X_I\subseteq X$ to be the set of all points $x\in X$ such that $x_v\neq x_w$ for every edge $(v,w)\in I$. These are open subsets, and the collection of all of them satisfies the finite intersection property. Since finite subgraphs of $G$ are all $C$-colorable, then none of the $X_I$’s are empty, hence there is an ultrafilter containing them. The ultrafilter convergence theorem implies there is a unique point $x\in X$ that the ultrafilter converges to, and one can check it is a proper $C$-coloring of $G$. (Without ultrafilters, one may use the fact that these $X_I$ sets are closed and have the finite intersection property, hence their intersection is nonempty.)

For the rest of this section, we’ll go for a direct proof that sort of combines Gottschalk’s approach and ultraproducts and expands out the definitions.

Let $G$ be a loopless planar graph, and let $\mathcal{F}G$ denote the set of all spanning subgraphs $H\subseteq G$ with finitely many edges (that is, $V(H)=V(G)$ and $E(H)$ is finite). By assumption, each $H\in \mathcal{F}G$ has a proper four coloring, hence there is a function $f_H:V(G) \to 4$ such that $f_H(v)\neq f_H(w)$ for every edge $(v,w)\in E(H)$. Consider the collection of sets of the form $A_H=\{H'\in \mathcal{F}G: H\subseteq H'\}$. This collection satisfies the finite intersection property since $A_{H}\cap A_{H'} = A_{H\cup H'}$ for each pair $H,H'\in \mathcal{F}G$. Since each $A_H$ is nonempty, this collection extends to an ultrafilter $U$ on $\mathscr{P}(\mathcal{F}G)$. Now we use the ultrafilter to “vote” on the coloring of $G$ itself in the following way.

For $v\in V(G)$, consider the function $F_v: \mathcal{F}G\to 4$ defined by $F_v(H) = f_H(v)$, and let $C(v)$ denote the set of colors $c\in 4$ such that $F_v^{-1}(c)\in U$. That is, $C(v)$ is the set of colors for which a “majority” of the spanning subgraphs chose that color for that vertex. A first fact is that $C(v)$ is nonempty. If it were empty, then for each $c\in 4$ we would have $\mathcal{F}G-F_v^{-1}(c)\in U$, and hence the intersection of all these complements would be in $U$. But

$$\begin{equation*} \bigcap_{i\in 4} \left(\mathcal{F}G-F_v^{-1}(i)\right) = \{H\in \mathcal{F}G : f_H(v) \not\in 4\} = \emptyset, \end{equation*}$$ and $U$ does not contain the empty set! A second fact is that $C(v)$ has at most one element. For $c,c'\in C(v)$, then we have $F_v^{-1}(c)\cap F_v^{-1}(c')\in U$. This intersection consists of all those graphs $H\in \mathcal{F}G$ such that $f_H(v)=c$ and $f_H(v)=c'$, hence $c=c'$ since the intersection is nonempty. Therefore, $\lvert C(v)\rvert=1$ for each $v\in V(G)$. Define $f: V(G)\to 4$ by letting $f(v)$ be the sole element of $C(v)$ for each $v$, which is to say $f$ is defined by the relation $F_v^{-1}(f(v))\in U$ for each $v\in V(G)$.

What is left is to show that $f$ defines a proper coloring.^[6] Let $(v,w)\in E(G)$ be an edge, and suppose it were the case that $c=f(v)=f(w)$. Let $H\in \mathcal{F}G$ be the graph with $E(H)=\{(v,w)\}$. Consider the intersection

$$\begin{equation*} A_H \cap F_v^{-1}(f(v)) \cap F_w^{-1}(f(w)) = \{H'\in \mathcal{F}G : (v,w)\in E(H')\text{ and } f_{H'}(v) = f_{H'}(w)\}. \end{equation*}$$ Since each $f_{H'}$ is a proper coloring, this set is empty. But, this is an intersection of three elements of $U$, so it would be an element of $U$ as well! Therefore $f$ must be a proper coloring, and we are done.

Remark. Define $F:\mathcal{F}G\to 4^{V(G)}$ by $f(H)=f_H$. Maps of sets carry ultrafilters to ultrafilters, which in particular means that $F_*U=\{A\subseteq 4^{V(G)}:F^{-1}(A)\in U\}$ is an ultrafilter on $4^{V(G)}$. Since $4^{V(G)}$ is compact Hausdorff, there is a unique $U$-limit of $F$ (that is, a limit point of $F_*U$), and it was the $f$ we constructed from before. With $\mathscr{P}G$ denoting the set of all spanning subgraphs of $G$, then we may endow it with the product topology using the correspondence that a spanning subgraph is a function $E(G)\to 2$. The subspace $\mathcal{F}G\subset\mathscr{P}G$ is dense, and $U$ converges to $G\in\mathscr{P}G$, which is outside $\mathcal{F}G$. Extending $U$ to be an ultrafilter on $\mathscr{P}G$, it is a principal ultrafilter generated by $G$, and the limit of a function with respect to a principal ultrafilter is the image of the generator.

3. By Kőnig’s lemma

One version of Kőnig’s lemma is that, given an infinite sequence $S_1,S_2,S_3,\dots$ of disjoint non-empty finite sets along with a relation $<$ on $\bigcup_i S_i$ such that for every $x\in S_{n+1}$ there is a $y\in S_n$ with $y<x$, then there exists an infinite sequence $x_1,x_2,x_3,\dots$ such that $x_n\in S_n$ for each $n$ with $x_1<x_2<x_3<\cdots$.

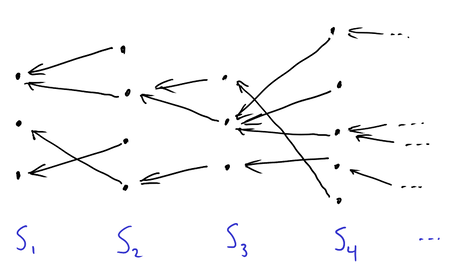
For example, given functions $f_n:S_{n+1}\to S_n$ for each $n$, we could define $y<x$ iff $y=f_n(x)$ for $y\in S_n$ and $x\in S_{n+1}$. We may interpret Kőnig’s lemma as saying the inverse limit $\varprojlim_n S_n$ is nonempty. Note that this is true even without each $f_n$ being surjective.

Nash-Williams^[7] points out how Kőnig’s lemma implies a version of infinite graph coloring in the case of a loopless planar graph $G$ with a countably infinite vertex set.

Since there are countably many vertices, we may define $n$-element subsets $V_n\subset V(G)$ with $V_n\subsetneq V_{n+1}$ for each $n\geq 1$ such that $V(G)=\bigcup_n V_n$. Let $G_n=G[V_n]$ be the subgraph of $G$ that is induced by the vertex set $V_n$; recall this means $G_n$ has all the edges of $G$ that are incident only to vertices from $V_n$. Let $S_n$ consist of all vertex colorings $V_n\to 4$ that are proper colorings for $G_n$. Since $G_n$ is a planar finite graph, $S_n$ is nonempty.

There is a function $f_n:S_{n+1}\to S_n$ defined by restricting the vertex coloring from $G_{n+1}$ to $G_n$. Hence, by Kőnig’s lemma there is a sequence $x_1,x_2,x_3,\dots$ with $x_n\in S_n$ for each $n$ and $f_n(x_{n+1})=x_n$. For any given vertex $v\in G$, there is an $n$ with $v\in V_n$. We may color $v$ according to $x_n$. We color all of $G$ in this way.

This must be a proper coloring because every pair of adjacent vertices is contained in some $V_n$ for a large enough $n$, and $V_n$ contains the edge between them.

The fact the inverse limit is non-empty in no way gives an effective algorithm. While each extension of the graph might be four-colorable, you might not be able to extend the four coloring itself, and it might change dramatically. All Kőnig’s lemma promises is that, with infinite foresight, you could make the right coloring decisions!